Bài tập trắc nghiệm Giải tích 12: Đường tiệm cận
Câu 1: Cho các mệnh đề sau
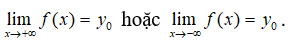
(2) Đường thẳng y = y 0 là đường tiệm cận ngang của đồ thị hàm số y = f(x) nếu
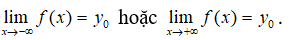
(3) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu
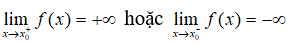
(4) Đường thẳng x = x 0 là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu
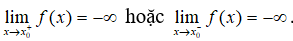
Trong các mệnh đề trên, số mệnh đề đúng là:
A.1 B. 2 C. 3 D. 4
Câu 2: Cho hàm số y = f(x) có
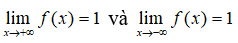
Trong các khẳng định dưới đây, khẳng định nào là đúng?
A. Đồ thị hàm số không có tiệm cận ngang.
B. Đồ thị hàm số có đúng một tiệm cận ngang.
C. Đồ thị hàm số có hai tiệm cận ngang là y = 1 và y = -1
D. Đồ thị hàm số có hai tiệm cận ngang là x = 1 và x = -1
Câu 3: Tìm tất cả các giá trị thực của m để đồ thị hàm số
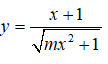
có hai tiệm cận ngang
A.Không tồn tại B. m < 0 C. m = 0 D. m > 0
Câu 4: Cho hàm số
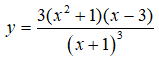
Trong các khẳng định sau, khẳng định nào đúng?
A. Đồ thị hàm số không có tiệm cận ngang.
B. Đồ thị hàm số có đúng một tiệm cận ngang.
C. Đồ thị hàm số có hai tiệm cận ngang là y = 3 và y = -1
D. Đồ thị hàm số có hai tiệm cận ngang là x = 3 và x = -1
Câu 5: Đồ thị hàm số
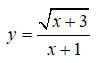
có tất cả bao nhiêu tiệm cận?
A. 0 B. 1 C. 2 D. 3
Câu 6: Hàm số nào sau đây có đồ thị nhận đường thẳng x = 0 làm tiệm cận đứng?
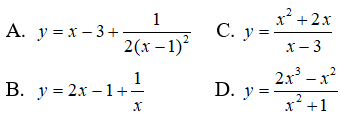
Hướng dẫn giải và Đáp án
1-C
|
2-B
|
3-D
|
4-B
|
5-C
|
6-B
|
Câu 1:
Dựa vào định nghĩa mệnh đề 1 sai và mệnh đề 2, 3, 4 đúng.
Câu 2:
Từ định nghĩa đồ thị hàm số có đúng một tiệm cận ngang là y=1
Câu 3:
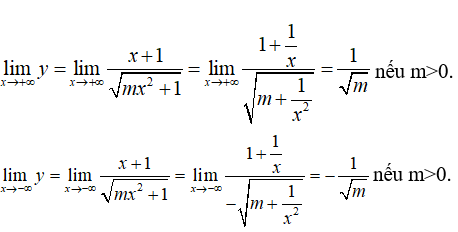
Để hàm số có hai tiệm cận ngang thì m > 0.
Câu 4:
Hàm số có đúng một tiệm cận ngang y=3.
Câu 5:
Vì x ≥ -3, nên ta chỉ xét trường hợp x → +∞
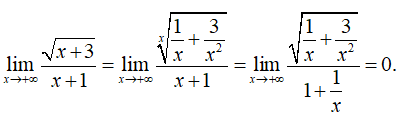
=> y = 0 là tiệm cận ngang của đồ thị hàm số.
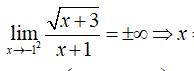
Câu 6:











 Copyright © 2021
Copyright © 2021