Bài tập trắc nghiệm Giải tích 12: Khảo sát sự biến thiên và vẽ đồ thị hàm số
Câu 6: Tiếp tuyến của parabol y = 4 - x2 tại điểm (1; 3) tạo với hai trục tọa độ một tam giác vuông. Diện tích tam giác vuông đó là
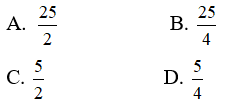
Câu 7: Cho hàm số y = 3x - 4x3 . Có nhiều nhất mấy tiếp tuyến với đồ thị hàm số đi qua điểm M(1; 3) ?
A. 1 B. 2 C. 3 D.4
Câu 8: Tìm m để phương trình x4 - 2x2 + 3 - m2 + 2m = 0 có đúng ba nghiệm phân biệt
A. m = -1 B. m = 3 C. -1 < m < 3 D. Cả A và B
Câu 9: Với m > 0 phương trình
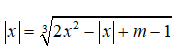
có ít nhất mấy nghiệm?
A. 0 B. 1 C. 2 D.3
Câu 10: Với mọi m ∈ (-1; 1) phương trình sin2 + cosx = m có mấy nghiệm trên đoạn [0; π] ?
A. 0 B. 1 C. 2 D.3
Hướng dẫn giải và Đáp án
6-B
|
7-B
|
8-D
|
9-A
|
10-B
|
Câu 6:
Ta có y’=-2x; y’(1)=-2. Phương trình tiếp tuyến của y = 4 - x2 tại điểm y(1,3) là
(d):y= -2(x-1)+3=-2x+5.
Đường thẳng (d) cắt trục hoành tại điểm A(5/2; 0) và cắt trục tung tại B(0;5).
Diện tích tam giác OAB vuông tại O là
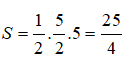
Câu 7:
Đường thẳng (d) có hệ số góc là k đi qua M(1;3) y=k(x-1)+3 .(d) tiếp xúc với đồ thì hàm số <=> hệ phương trình có nghiệm
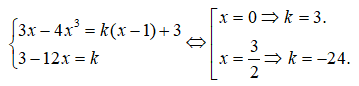
Do đó có tối đa hai tiếp tuyến đi qua điểm M(1;3).
Câu 8:
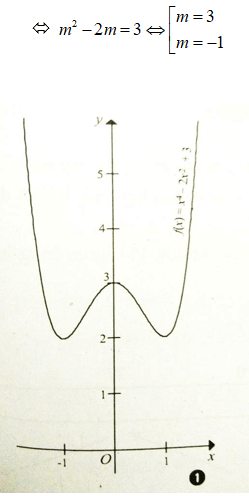
Xét hàm số y = x4 - 2x2 + 3 ( C )
Đồ thị có dạng như hình (1)
x4 - 2x2 + 3 -m2 + 2m = 0 có đúng ba nghiệm phân biệt <=> Đường thẳng y = m2 + 2m cắt đồ thị C tại ba điểm phân biệt
Câu 9:
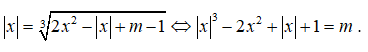
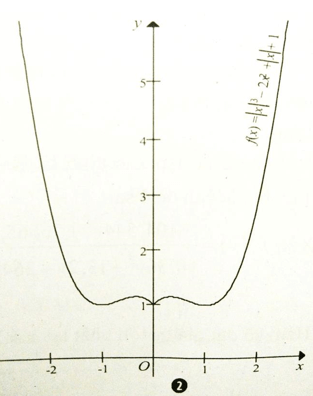
Đồ thị hàm số y = |x|3 - 2x2 + |x| + 1 có dạng như hình (2)
Dựa vào đồ thị với m > 0 phương trình có tối thiểu 0 nghiệm.
Câu 10:
sin2x + cosx = m <=> -cosx2x + cosx + 1 = 0
Đặt t= cos x =>
=>f’(t)=-2t+1.
Do x ∈ [0; π] => t ∈ [-1; 1]
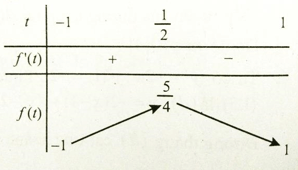
Từ bảng biến thiên ta có m ∈ (-1; 1) thì f(t)=m có một nghiệm










 Copyright © 2021
Copyright © 2021