Bài tập trắc nghiệm Giải tích 12: Khảo sát sự biến thiên và vẽ đồ thị hàm số
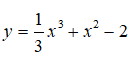
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình y'' = 0 là
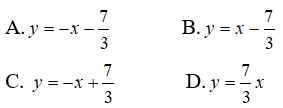
Câu 7: Cho hàm số
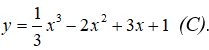
Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng y = 3x -1
A. y = 3x + 1 B. y = 3x - 29/3 C. 3x + 20 D. Cả A và B đúng
Câu 8: Gọi M, N là giao điểm của
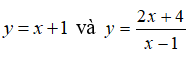
Khi đó hoành độ trung điểm của I của đoạn thẳng MN bằng
A. 2 B.1 C. 0 D. -1
Câu 9: Tìm m để phương trình x3 + 3x2 = m có ba nghiệm phân biệt
A. m > 4 B. m < 0 C. 0 ≤ m ≤ 4 D. 0 < m < 4
Hướng dẫn giải và Đáp án
6-A
|
7-D
|
Câu 6:
Ta có
y' = x2 + 2x; y'' = 2x + 2 => y'' = 0 <=> x = -1 => -4/3, y'(-1) = -1
Phương trình tiếp tuyến của đồ thị hàm số tại điểm x = -1 là:
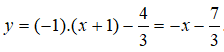
Chọn đáp án A.
Câu 7:
Ta có y' = x2 - 4x + 3. Tiếp tuyến của đồ thị (C) song song với đường thẳng y = 3x - 1 nên hệ số góc của tiếp tuyến là k = 3.
Xét y' = 3 <=> x2 - 4x = 0
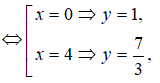
Phương trình tiếp tuyến của đồ thị tại A(0;1) có hệ số góc k = 3 là y = 3x + 1
Phương trình tiếp tuyến của đồ thị tại B(4; 7/3) có hệ số góc k = 3 là y = 3x - 29/3 .
Chọn đáp án D.
Câu 8:
Xét phương trình hoành độ giao điểm
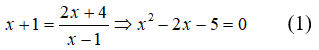
Giao điểm của hai đồ thị hàm số là M(x1; y1), N(x2; y2) với x1, x2 là nghiệm phương trình (1). Do đó
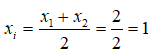
Chọn đáp án B.
Câu 9:
Xét hàm số
y = f(x) = x3 + 3x2 (C)
Đồ thị hàm số có dạng như hình bên.
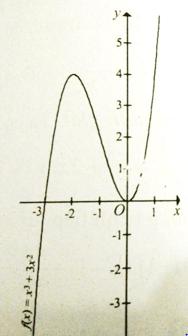
x3 + 3x2 = m có ba nghiệm phân biệt
<=> Đường thẳng y = m cắt đồ thị (C) tại ba điểm phân biệt <=> 0 < m < 4
Chọn đáp án D.










 Copyright © 2021
Copyright © 2021