Bài tập trắc nghiệm Giải tích 12: Hàm số lũy thừa

A. max y = 2∜2 , min y=1. B. max y = 2∜2 , min y = ∜2 .
C. max y=48, min y=19. D. max y = ∜8 , min y = ∜2 .
Câu 15: Tìm các giá trị lớn nhất và nhỏ nhất của hàm số y = x2/3(20 - x) trên đoạn [1; 10]
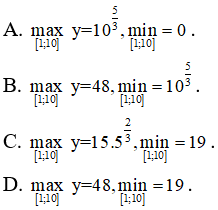
Câu 16: Với là một số thực dương và hàm số
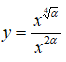
nghịch biến trên khoảng (0; +∞). Khẳng định nào sau đây là đúng?
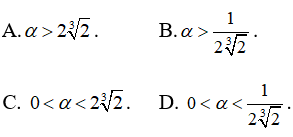
Câu 17: Số nào lớn nhất trong các số được liệt kê trong bốn phương án A,B,C,D dưới đây?

Câu 18: Tìm đạo hàm của hàm số
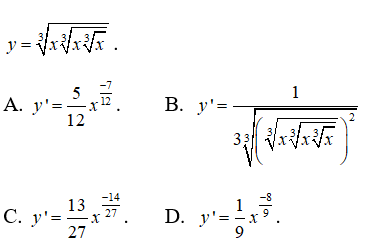
Câu 19: Số nào lớn nhất trong các số được liệt kê trong bốn phương án A,B,C,D dưới đây?
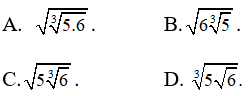
Câu 20: Cho a và b là hai số dương. Tìm giá trị lớn nhất của hàm số y = xa(1 - x)b trên [0;1].
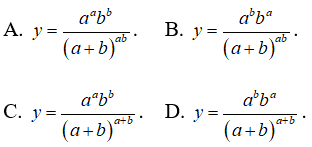
Hướng dẫn giải và Đáp án
14-C
|
15-D
|
16-B
|
17-D
|
18-C
|
19-B
|
20-D
|
Câu 14:
Tập xác định D = [0; 1]
Ta có:
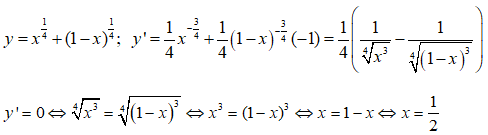
y(0) = y(1) = 1; y(1/2) = ∜8. Từ đó max y = y(1/2) = ∜8, min y = y(0) = 1
Câu 15:
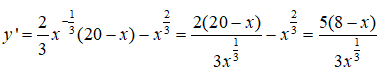
y' = 0 <=> x = 8
Ta có: y(1) = 19, y(8) = 48, y(10) = 105/3 ≈ 46,6 > 19
Từ đó:
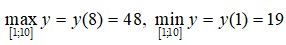
Câu 16:
Hàm số
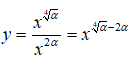
nghịch biến trên (0; +∞) nên ∜α - 2α < 0
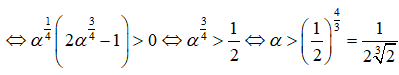
Câu 17:
Viết lại các số dưới dạng cùng căn bậc 4:
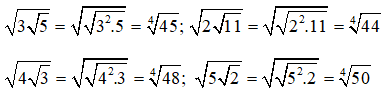
Từ đó ta thấy 5√2 là lớn nhất
Câu 18:
Viết lại
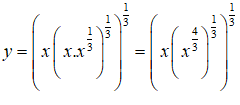
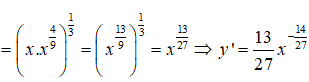
Câu 19:
Viết lại các số
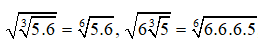
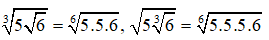
Từ đó ta thấy số lớn nhất là
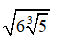
Câu 20:
y' = xa - 1(1 - x)b - 1(a - ax - bx). Trên khoảng (0 ;1)

Ta có: y(0) = y(1) = 0;
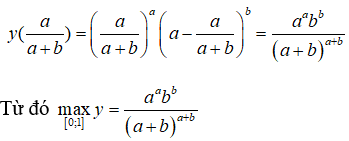










 Copyright © 2021
Copyright © 2021