Bài tập trắc nghiệm Giải tích 12: Hàm số lũy thừa (Phần 2)
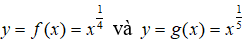
lần lượt tại hai điểm A và B. Biết rằng tung độ điểm A bé hơn tung độ điểm B. Khẳng định nào sau đây là đúng?
A. 0 < α < 1 B. α > 1 C. 1/5 < α < 4 D. 1/4 < α < 5
Câu 7: Cho hàm số
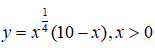
Khẳng định nào sau đây là đúng?
A. Hàm số ngịch biến trên (0;2).
B. Hàm số ngịch biến trên khoảng (5; +∞) .
C. Hàm số đồng biến trên (2; +∞) .
D. Hàm số không có điểm cực trị nào.
Câu 8: Tìm các điểm cực trị của hàm số
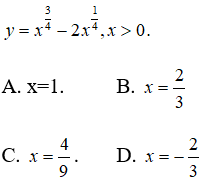
Câu 9: Tìm các điểm cực trị của hàm số
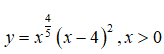
A. x=4 và x = 8/7 . B. x=4. C. x=2. D. x=2 và x = 4/9 .
Câu 10: Tìm giá trị lớn nhất và nhỏ nhất của hàm số
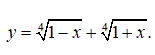
A. max y = 2√2 , min y = ∜2 . B.max y=2, min y=0.
C. max y = 2√2 , min y=0 D.max y=2, min y= ∜2 .
Hướng dẫn giải và Đáp án
6-A
|
7-B
|
8-C
|
9-A
|
10-D
|
Câu 6:
Từ giả thiết suy ra f(α) < g(α)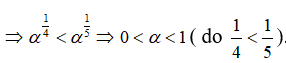
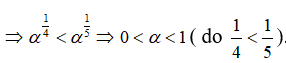
Chọn đáp án A.
Nhận xét. Ở đây ta sử dụng tính chất:
Nếu a > 1 thì aα > aβ <=> α > β ;
Nếu 0 < α < 1 thì aα > aβ <=> α < β .
Học sinh có thể không áp dụng tính chất trên mà giải tiếp:
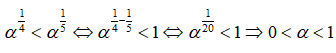
Câu 7:
Ta có
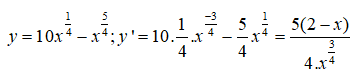
Ta thấy y'(x) < 0 <=> x > 2 nên hàm số nghịch biến trên (2; +∞) , và do đó, hàm số nghịch biến trên (5; +∞) .
Chọn đáp án B.
Câu 8:
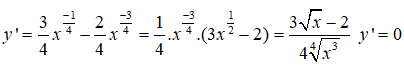
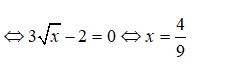
y’ đổi dấu khi qua điểm x = 4/9 nên hàm số có một điểm cực trị là x = 4/9 .
Chọn đáp án C.
Câu 9:
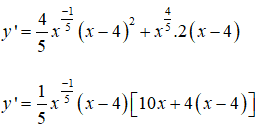
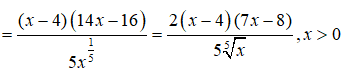
y’=0 <=> x = 4 hoặc x = 8/7 ,
Ta thấy y’ đổi dấu khi đi qua 2 điểm x=4 và x = 8/7 nên đây là 2 điểm cực trị của các hàm số đã cho.
Chọn đáp án A.
Câu 10:
Tập xác định D = [-1;1]. Viết lại
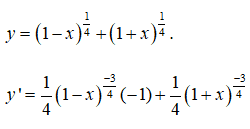
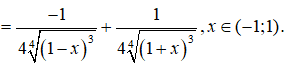
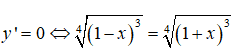
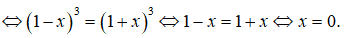
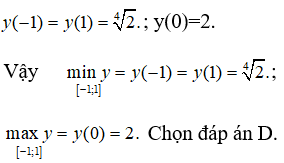










 Copyright © 2021
Copyright © 2021